BIJAX - Bayesian Inference in JAX

• Contributed to an open-source Python library with a unified and transparent approach for various distribution approximation techniques such as Laplace Approximation and Markov Chain Monte Carlo (MCMC) sampling.
• Reinforced the approximation methods by adding extensive functionalities such as Full rank, Low rank, Mean Field, Subnetwork, Last Layer, and Kronecker-Factored Approximate Curvature (KFAC).

Quick Links:

• GitHub
• Report

Laplace Approximation

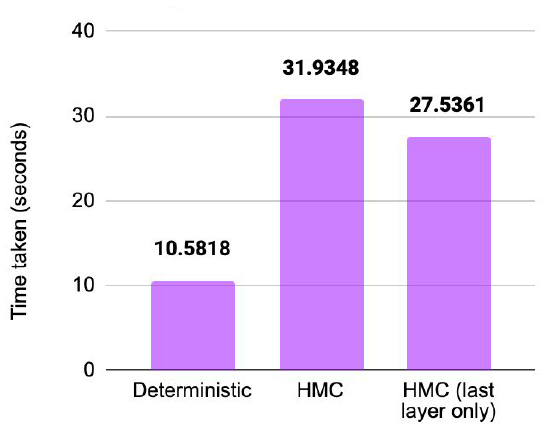
The results of Laplace Approximation for fully bayesian network, last-layer bayesian network, and subnet bayesian network are shown in the figures below.

Laplace Approximation using all layers for regression on a 2D dataset. MAP, fullrank, lowrank, diag, kron (left to right)

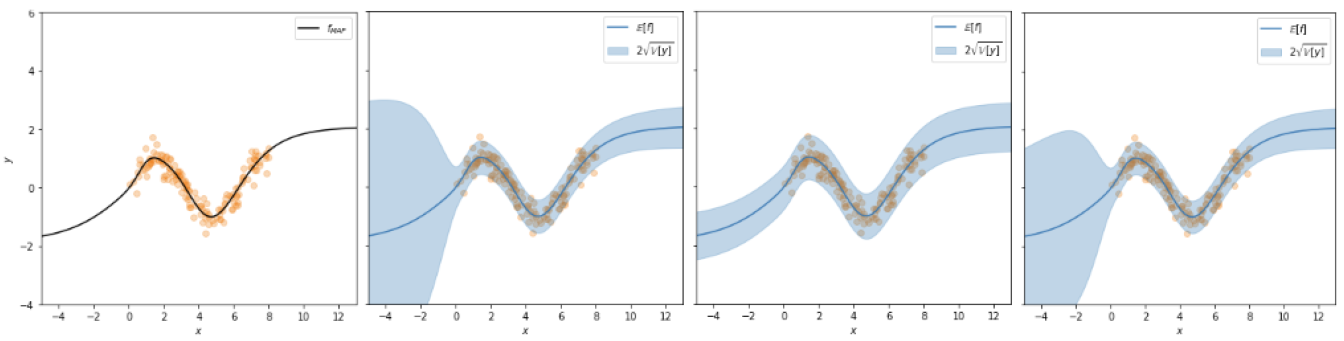
Laplace Approximation using last layer for regression on a 2D dataset. MAP, fullrank, diag, kron (left to right)

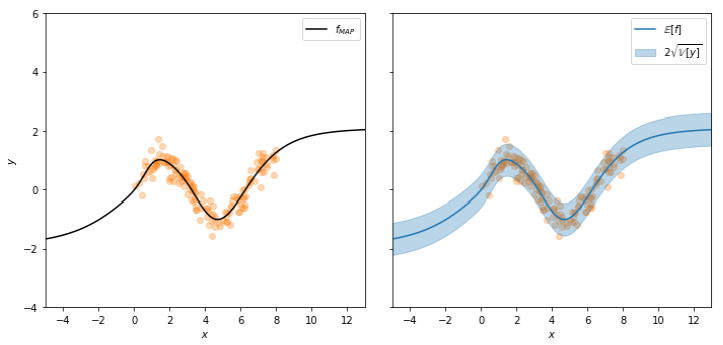
Laplace Approximation using subnetwork for regression on a 2D dataset. MAP, fullrank (left to right)

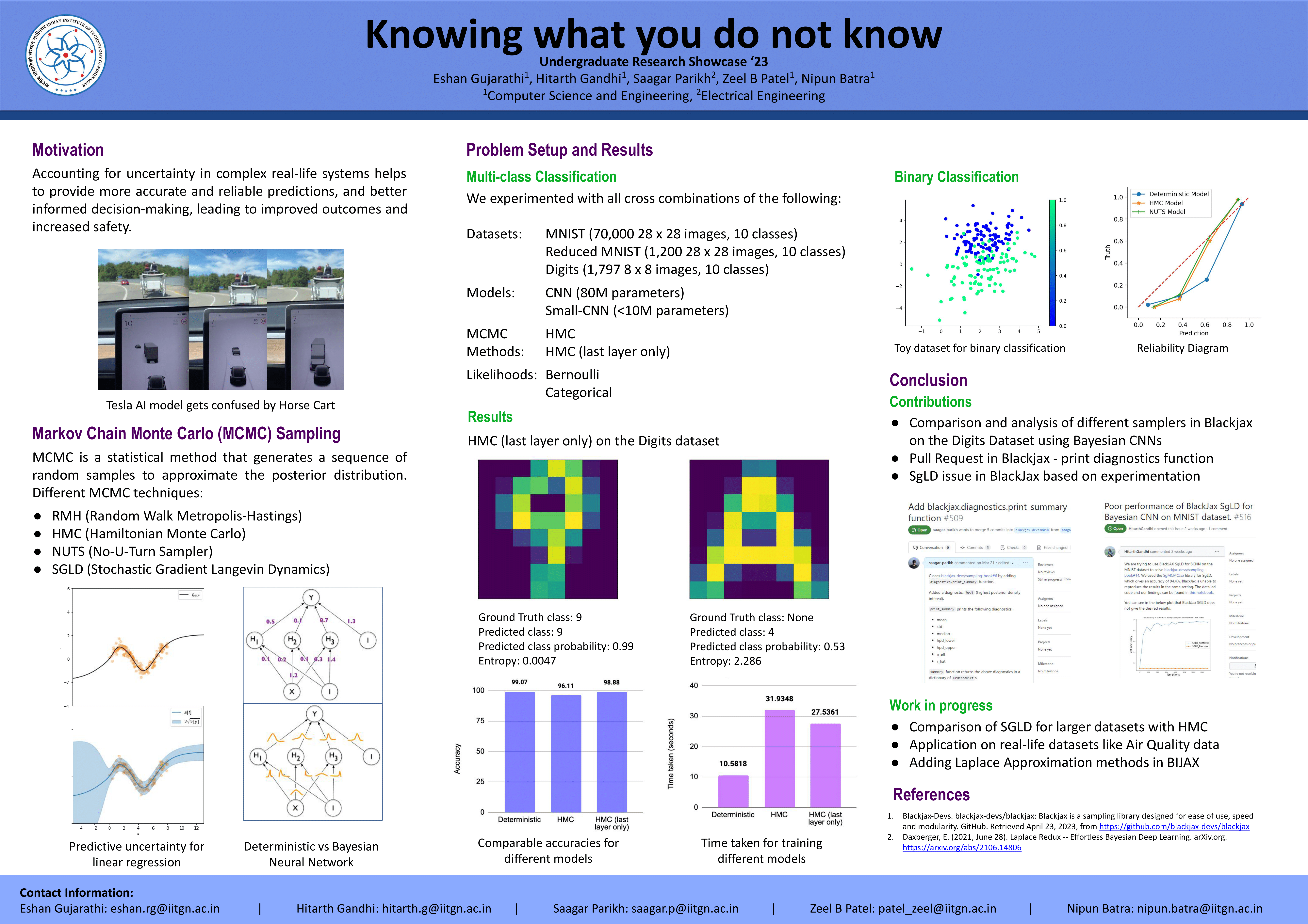
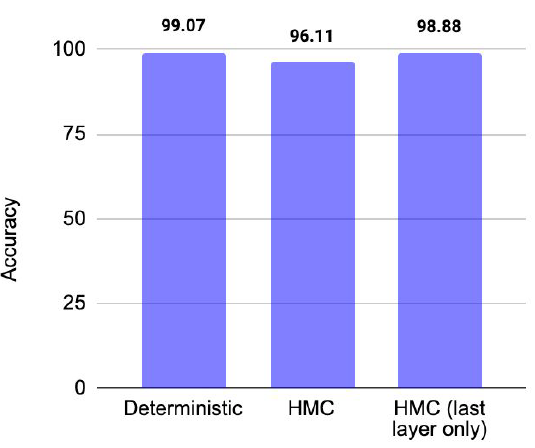
Hamiltonian Monte Carlo (HMC) on the Digits dataset

For the case of out of distribution data (the letter ‘A’ is out of distribution for a dataset of digits), a deterministic model, would predict a class with a certain confidence. We define an uncertainty metric ‘entropy’ which provides information on how uncertain the model is (higher is more uncertain). The results below show that the HMC model predicts a class with low confidence and high entropy.

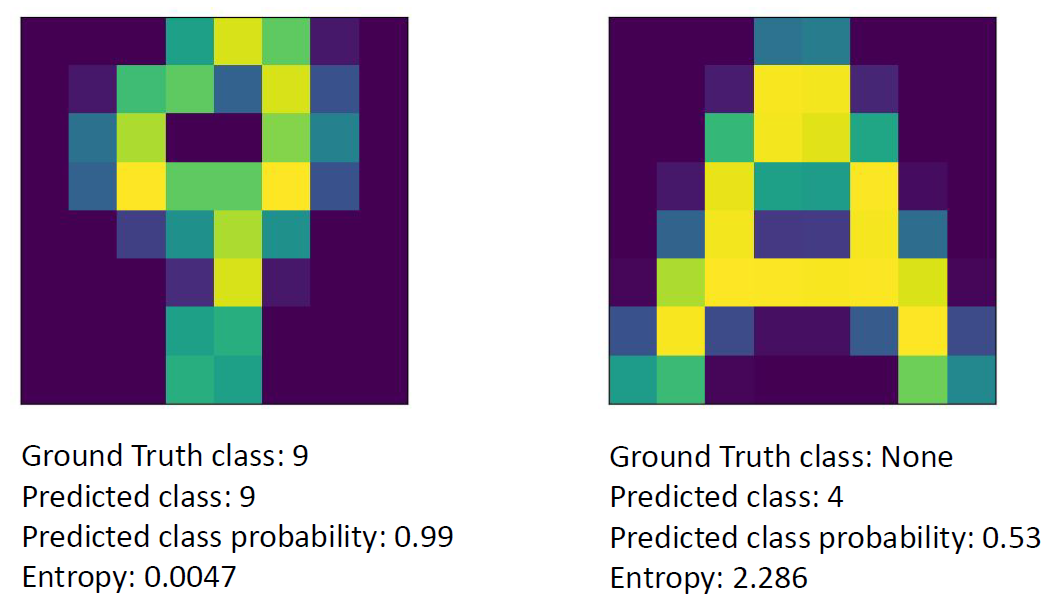
Ground Truth, Predicted Class, Predicted Class Probability and Entropy

Accuracy and Timing Analysis

Poster